Optimizing Rank for High-Fidelity Implicit Neural Representations

Preprint

Julian McGinnis1,2, Florian Hölzl3, Suprosanna Shit4,5, Florentin Bieder6, Paul Friedrich6, Mark Mühlau1, Björn Menze4, Daniel Rueckert1,3, Benedikt Wiestler2,3
1TUM 2MCML 3HPI 4University of Zurich
5ETHZ AI Centre 6University of Basel
arXiv Code (soon) Colab (soon)

Rank preservation overcomes the low-frequency bias of ReLU MLPs. Vanilla ReLU MLPs lack high-frequency detail (top). Orthogonalized, rank-preserving weight updates enable them to achieve faithful high-frequency reconstructions (middle) by maintaining a stable layer rank throughout optimization (illustrated for hidden layers trained with Adam, which exhibits rank collapse, versus Muon, which preserves stable rank; bottom)

Abstract

Implicit Neural Representations (INRs) based on vanilla Multi-Layer Perceptrons (MLPs) are widely believed to be incapable of representing high-frequency content. This has directed research efforts towards architectural inter- ventions, such as coordinate embeddings or specialized activation functions.

In this paper, we challenge the notion that the low-frequency bias of vanilla MLPs is an intrinsic, architectural limitation, but instead a symptom of stable rank degradation during training. We empirically demonstrate that regulating the network's rank during training substantially improves the fidelity of the learned signal, rendering even simple MLP architectures expressive.

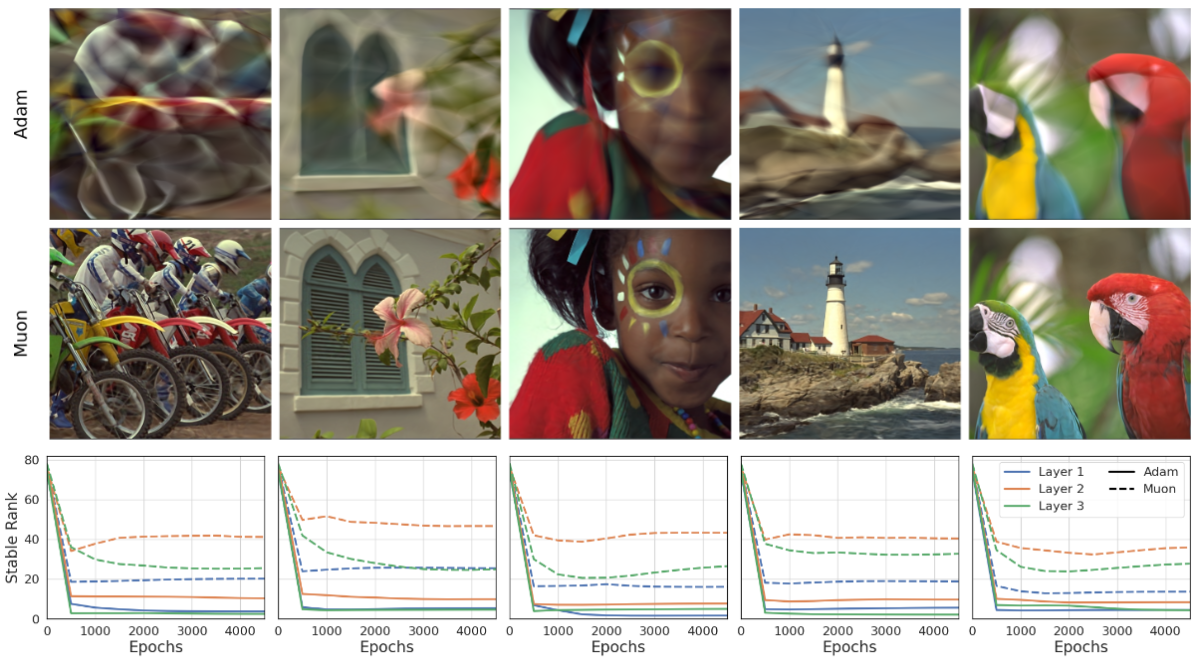
Extensive experiments show that using optimizers like Muon, with high-rank, near-orthogonal updates, con- sistently enhances INR architectures even beyond simple ReLU MLPs. These substantial improvements hold across a diverse range of domains, including natural and medical images, and novel view synthesis, with up to 9 dB PSNR improvements over the previous state-of-the-art.

A Stable Rank Perspective on Spectral Bias

The phenomenon of spectral bias describes how neural networks prioritize low-frequency functions during training. Rather than analyzing this in the function's Fourier spectrum, we examine how it arises from the linear-algebraic structure linking activations and weights through gradients. Based on the stable rank of layer updates, we clarify how activations shape layer weights, why this reinforces a low-frequency bias in INRs, and how different interventions address this bias.

Stable Rank and Model Expressiveness

To quantify the effective dimensionality of this process, we use the stable rank \(s(A)\) as a numerically stable measure of diversity for a matrix \(A\) with singular values \(\sigma_{i}\):

$$ s(A) = \frac{\|A\|_F^2}{\|A\|_2^2} = \frac{\sum_i \sigma_i^2}{\sigma_{\max}^2} $$

A rank-1 matrix has \(s(A)=1\), while a semi-orthogonal matrix with rank \(k\) has \(s(A)=k\). Applying this inequality to the batched gradient \(\nabla_{W_{l}}\mathcal{L}=G_{l+1}H_{l}^{\top}\) gives:

$$ s(\nabla_{W_{l}}\mathcal{L}) \le \text{rank}(H_{l}) $$

Thus, for a single layer, it is crucial to understand that the input activations constrain the effective dimensionality of the update and consequently its capacity to explore the layer's weight space.

Interventions to Increase Stable Rank

Based on this insight, we provide a unifying framework that explains the effectiveness of common architectural modifications in INRs. We group these interventions into broad categories of architectural modifications.

1. Input-Level Interventions
(e.g. Fourier Features)

Methods such as Fourier Features map the low-dimensional input coordinate \(x\) to a high-dimensional vector \(\gamma(x)\) using sampled random frequencies.

  • Mechanism: This expands the batch matrix \(H_{0}\) to \(H^{\prime}=\gamma(H_{0})\).
  • Result: This increases the stable rank bound on the first-layer update \(s(\nabla_{W_{1}}\mathcal{L})\le \text{rank}(H_{0}^{\prime})\), enabling learning of higher-frequency components.
  • Limitation: The trade-off is that frequency bands are static and hand-engineered, potentially not matching the data and/or task.

2. Activation-Level Interventions
(e.g. SIREN, BatchNorm)

A direct approach targets the activations themselves to counter rank diminishing with depth.

  • Mechanism: Normalization, particularly Batch Normalization (BN), or modifying activation functions (e.g. \(sin(\cdot)\) in SIREN) can promote high-frequency learning.
  • Result: Effectively increasing \(\text{rank}(H_{l})\).
  • Limitation: Requires specialized initialization to maintain gradient stability or greater tuning complexity.

3. Optimizer-Level Intervention
(Muon)

We instead view this challenge as an optimization problem, calling for direct intervention at the update level.

  • Mechanism: We propose to explicitly enforce isotropy in the gradient updates to increase expressiveness. This can be achieved with the general class of orthogonalizing optimizers.
  • Formula: We map \(U\) to the Frobenius-nearest semi-orthogonal matrix: $$ \text{Ortho}(U)=\arg \min_{O}||O-U||_{F} $$
  • Result: This forces the weight parameter update to be distributed evenly across all of its singular directions.

High-Resolution Reconstruction

Tiger Reconstruction

Reconstructing a tiger from the animal AFHQ dataset using a vanilla ReLU MLP and different rank-preserving/inducing methods. We propose to use Muon, which induces a high stable rank via its orthogonalized weight updates.

Sparse-View CT Reconstruction

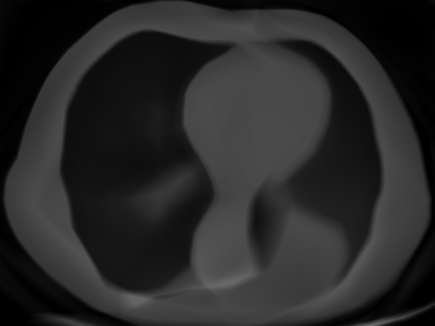
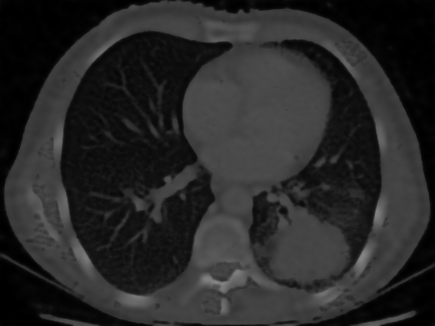
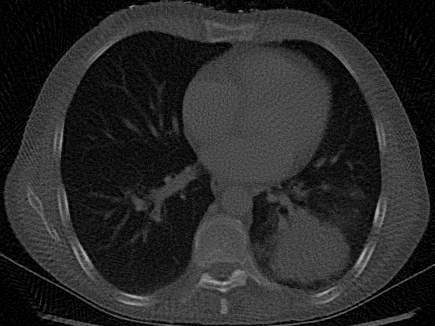
We reconstruct a chest CT from only 100 sparse projections. Optimization with Muon significantly reduces streak artifacts and recovers fine anatomical structures (such as bronchi) compared to Adam.

ReLU MLP

ReLU MLP Adam ReLU MLP Muon

ReLU FFN

ReLU FFN Adam ReLU FFN Muon

Real WIRE

Real WIRE Adam Real WIRE Muon

Single Image Super Resolution (SISR)

We compare the reconstruction fidelity of various implicit architectures when optimized with Adam versus Muon. Drag the slider to observe how rank-preserving optimization recovers high-frequency details (e.g., textures, edges) that are smoothed out by Adam.

ReLU MLP

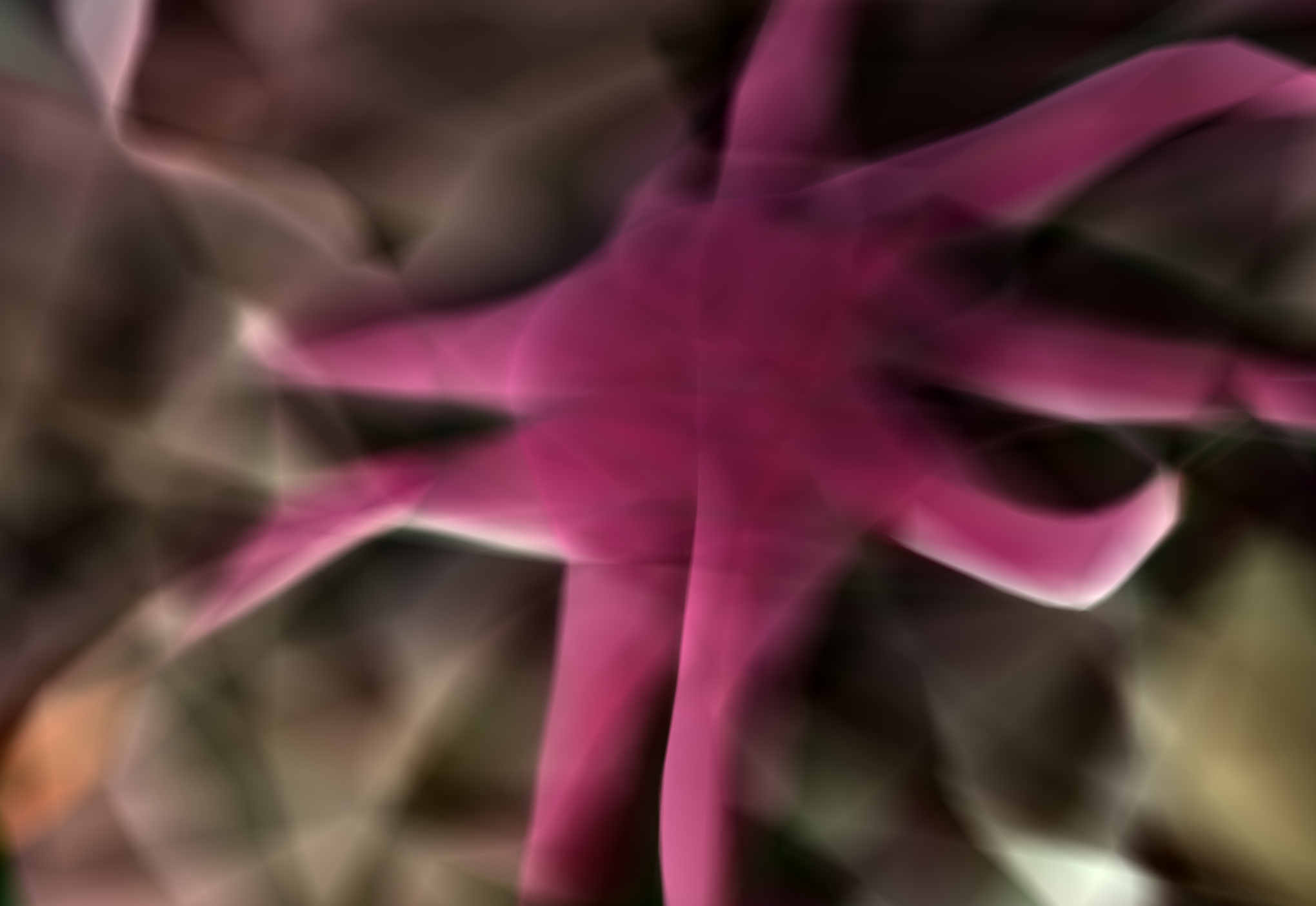
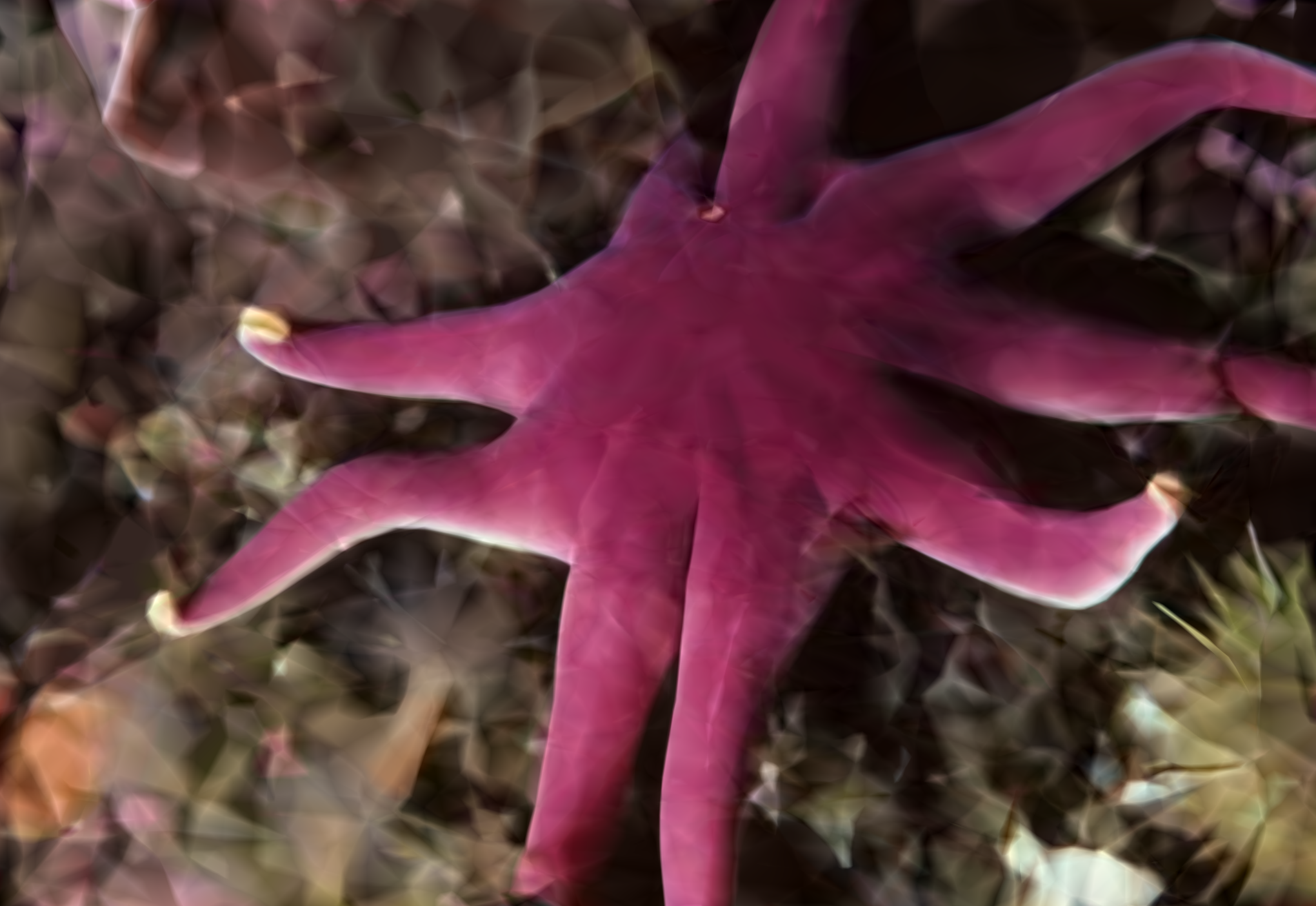
ReLU MLP Adam ReLU MLP Muon

ReLU FFN

ReLU FFN Adam ReLU FFN Muon

Gaussian MLP

Gaussian MLP Adam Gaussian MLP Muon

SIREN

SIREN Adam SIREN Muon

Finer MLP

Finer MLP Adam Finer MLP Muon

3D Shape Reconstruction

We compare the reconstruction of 3D signed distance fields (SDFs) using a standard ReLU MLP. Muon captures sharp geometric features that are smoothed by Adam.

Armadillo (ReLU MLP)

Armadillo Adam Armadillo Muon

Statue (ReLU MLP)

Statue Adam Statue Muon

Novel View Synthesis (NeRF)

Chair

Comparisons on the Chair scene. Muon (right video in each pair) produces sharper, more geometrically consistent renderings with fewer "cloudy" artifacts than Adam.

ReLU MLP

Adam
Muon

FINER

Adam
Muon

Drums

Comparisons on the Drums scene. Similarly, Muon demonstrates superior high-frequency detail reconstruction and geometry compared to Adam.

ReLU MLP

Adam
Muon

FINER

Adam
Muon

BibTeX

      
@article{mcginnis2025optimizing,
         title={Optimizing Rank for High-Fidelity Implicit Neural Representations},
         author={McGinnis, Julian and Hölzl, Florian and Shit, Suprosanna and Bieder, Florentin and Friedrich, Paul and Mühlau, Mark and Menze, Björn and Rueckert, Daniel and Wiestler, Benedikt},
         journal={arXiv preprint TBD},
         year={2025}
        }

Acknowledgements

This work is funded by the Munich Center for Machine Learning. Julian McGinnis and Mark Mühlau are supported by Bavarian State Ministry for Science and Art (Collaborative Bilateral Research Program Bavaria – Quebec: AI in medicine, grant F.4-V0134.K5.1/86/34). Suprosanna Shit is supported by the UZH Postdoc Grant (K-74851-03-01). Suprosanna Shit and Björn Menze acknowledge support by the Helmut Horten Foundation.